Statement

We have four types of tiles: an L trimino, an S tetromino, a Z tetromino, and an O tetromino, as shown below. Note that L is just a trimino.

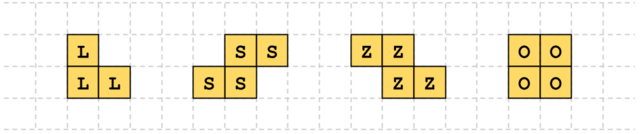
We want to use the tiles to tile an \(n\times n\) square perfectly (every cell covered exactly once, nothing sticking out). Each piece can be rotated by multiples of 90 degrees while doing so.

We have a sufficient supply of tiles of each type. The available tetrominos are free, but we have to pay one coin for each trimino we use.

For a given \(n\), determine whether a perfect tiling exists, and if it does, produce a bitmap of one perfect tiling that is as cheap as possible.

Input format

The first line of the input file contains the number \(t\) of test cases. The specified number of test cases follows, one after another.

Each test case consists of a single line containing a single number \(n\). The values of \(n\) are given in increasing order.

Output format

Print an answer for each test case.

If there is no valid tiling, output a single line with the string “NO” (quotes for clarity).

If there are some valid tilings, pick any one of the cheapest valid tilings and output \(n+1\) lines: first a line with the string “YES” and then \(n\) lines with \(n\) characters each, encoding the tiling.

The tiling should be output as a bitmap of lowercase English letters (a-z). Squares belonging to the same tile should be represented by the same letter. Tiles that touch by side should be represented by distinct letters.

Subproblem T1 (15 points, public)

Input file: T1.in

In this subproblem \(t=6\) and the six tests are \(n=1..6\).

Subproblem T2 (30 points, public)

Input file: T2.in

In this subproblem \(t=10\) and the ten tests are \(n=1..10\).

Subproblem T3 (55 points, secret)

Input file: T3.in

In this subproblem each \(n\) is at most 150 and \(\sum n^2\leq 100\,000\) (to guarantee that the output is small enough to upload).

Example

2
3
11

NO
YES
aaxxaaxxaax
aoxfaoxfaxx
xooffooffaa
xxaaxxaaxao
ooaoxfaxxoo
oxxooffaaxx
axffaaxaoox
aafxaoxxoaa
ooxxfooaaxa
oaoffafaxxo
aaooaaffxoo

Please note that the output shown above for \(n=11\) is syntactically correct but intentionally not optimal.